最近、ベイズ統計に触れる機会があるのですが、いまいち胸に落ちる感じがしません。数式がダメなら、お話から入ってみようと思い上記の本を読んでみました。
すると、すごい分かりやすい(気がする)。ベイズの定理を再発見したラプラスの着想を、本書では下記のように表現してます(C:原因,E:結果,P:確率)。
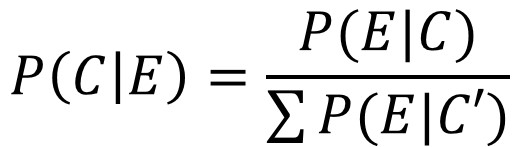
ここでP(C|E)はある結果のデータEが得られた時にCが原因である確率。P(E|C)は出来事Cが真実である場合に、結果のデータEが得られる確率。分母は原因で有りうる全ての事象C'についてデータEが得られる確率の合計。
ベイズの定理的に表現すると、P(C|E)は事後分布、P(E|C)は尤度です。
膨大にある天文学データの誤差を分析する必要性から、ラプラスは確率論に接近したというのも面白いですね。
(追記:2015.06.19)
地球物理学者のハロルドジェフリーズという人に関する記述で、頻度主義のp値が批判されています。ここを読んで、頻度主義しか統計学で学んでこなかった自分はベイズ主義の利点が感覚的に分かってきました。真の値が確率的、分布するという点が肝なのね。長いけど、下に引用。
ジェフリーズは、頻度主義者たちが起きる可能性はあっても実際に起きていない結果についてあれこれ考えるのを見て、じつに妙な話だと思った。自分だったら、地震で起きた津波の到達時間に関する情報をもとにして、特定の地震の震央に関する自分の仮説が正しい確率がどれくらいになるのかを知りたいところだが…。なぜ結果でありえたが実際には起きていない事柄を拠り所にして、仮説を捨て去らねばならないのだろう。(略)しかもp値はデータに関する言明であって、ジェフリーズが知りたいのは、データを前提とした仮説の正しさに関する言明なのだ。(p.112)
確かに、フィッシャーの方法によって退けられた仮説の一部にせよ、調べてみる価値があったり、実際に正しかったという可能性は排除できない。(p.113)
