行列モデルを用いた個体群レベルの生態毒性評価について(参考:こちら)。
個体群の増加率(population growth rate)に対する各生活史変量aij(vital rates)の感度(sensitivity)は下の式で求められます。
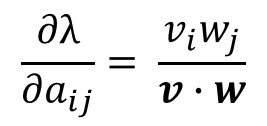
ここでw,vはそれぞれ射影行列の右側固有ベクトル、左側固有ベクトルを示しています。v・wはそれぞれの内積です。viはvの第i成分を示しています。
フリーの統計ソフトウェアRでこの感度を求める練習をします。射影行列は田中と中西(1998)のニジマスのデータを使います。まず最大固有値λ、すなわち個体群増加率を求めましょう。
> B <- matrix(c(0,0.1,0,0,0,0,0, 31,0,0.31,0,0,0,0, 199,0,0,0.29,0,0,0, 1778,0,0,0,0.144,0,0, 2734,0,0,0,0,0.154,0, 4685,0,0,0,0,0,0.15, 5424,0,0,0,0,0,0), nrow=7,ncol=7)
> B
[,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] 0.0 31.00 199.00 1778.000 2734.000 4685.00 5424
[2,] 0.1 0.00 0.00 0.000 0.000 0.00 0
[3,] 0.0 0.31 0.00 0.000 0.000 0.00 0
[4,] 0.0 0.00 0.29 0.000 0.000 0.00 0
[5,] 0.0 0.00 0.00 0.144 0.000 0.00 0
[6,] 0.0 0.00 0.00 0.000 0.154 0.00 0
[7,] 0.0 0.00 0.00 0.000 0.000 0.15 0
> lamda <- eigen(B)$values [1]
[1] 2.760164+0i
次に右固有ベクトルwと左固有ベクトルvを求めます。左固有ベクトルvは、射影行列Bの転置行列BTの右固有ベクトルとして求めます。
> w<- eigen(B)$vectors[,1]
> w
[1] -9.993360e-01+0i -3.620567e-02+0i -4.066337e-03+0i -4.272346e-04+0i
[5] -2.228918e-05+0i -1.243597e-06+0i -6.758279e-08+0i
> v<-eigen(t(B))$vectors[,1]
> v
[1] -0.000336702+0i -0.009293529+0i -0.049077106+0i -0.236059218+0i
[5] -0.367402982+0i -0.607462741+0i -0.661653283+0i
念のため、wとvが右固有ベクトルと左固有ベクトルとなっているか確認します。固有ベクトルの定義からBw=λwまたはvB=λvが成り立てばOKです。
> B%*%w
[,1]
[1,] -2.758331e+00+0i
[2,] -9.993360e-02+0i
[3,] -1.122376e-02+0i
[4,] -1.179238e-03+0i
[5,] -6.152179e-05+0i
[6,] -3.432533e-06+0i
[7,] -1.865396e-07+0i> diag(eigen(B)$values[1],ncol=7, nrow=7)%*%w #λEwをおこなっている
[,1]
[1,] -2.758331e+00+0i
[2,] -9.993360e-02+0i
[3,] -1.122376e-02+0i
[4,] -1.179238e-03+0i
[5,] -6.152179e-05+0i
[6,] -3.432533e-06+0i
[7,] -1.865396e-07+0i#次はvについて
> v%*%B
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] -0.0009293529+0i -0.02565167+0i -0.1354609+0i -0.6515622+0i -1.014093+0i -1.676697+0i
[,7]
[1,] -1.826272+0i> v%*% diag(eigen(B)$values[1],ncol=7, nrow=7)
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] -0.0009293529+0i -0.02565167+0i -0.1354609+0i -0.6515622+0i -1.014093+0i -1.676697+0i
[,7]
[1,] -1.826272+0i
ようやく感度解析をおこないます。まず齢0から齢1への成長率に対する感度。
> v[2]*w[1]/(v%*%w)
[,1]
[1,] 9.454101+0i
なぜでしょう。論文の値(0.66)と全然異なります。論文の値が感度ではなくelasticityを示しているのかと思いきや、そうでもないです。うーむ、分からん。
> v[2]*w[1]*0.1/lamda/(v%*%w)
[,1]
[1,] 0.3425195+0i
(追記 2015.02.17)
ネット上にあった東邦大の資料で確認してみたところ、自分の方法で問題なさそう。ハイイロリスのレスリー行列というもの。
> L <- matrix(c(0.32,0.46,0,0,0,0,0, 0.57,0,0.77,0,0,0,0, 0.57,0,0,0.65,0,0,0, 0.57,0,0,0,0.67,0,0, 0.57,0,0,0,0,0.64,0, 0.57,0,0,0,0,0,0.88, 0.57,0,0,0,0,0,0), nrow=7,ncol=7)
> L
[,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] 0.32 0.57 0.57 0.57 0.57 0.57 0.57
[2,] 0.46 0.00 0.00 0.00 0.00 0.00 0.00
[3,] 0.00 0.77 0.00 0.00 0.00 0.00 0.00
[4,] 0.00 0.00 0.65 0.00 0.00 0.00 0.00
[5,] 0.00 0.00 0.00 0.67 0.00 0.00 0.00
[6,] 0.00 0.00 0.00 0.00 0.64 0.00 0.00
[7,] 0.00 0.00 0.00 0.00 0.00 0.88 0.00> e1<- eigen(L)$vectors[,1]
> e1
[1] 0.85268485+0i 0.37769273+0i 0.28004099+0i 0.17527792+0i 0.11308221+0i
[6] 0.06968936+0i 0.05905293+0i
> e2<- eigen(t(L))$vectors[,1]
> e2
[1] -0.3207554+0i -0.5010080+0i -0.4382698+0i -0.4189446+0i -0.3764845+0i
[6] -0.3252339+0i -0.1760520+0i
#感度行列は下のようになる
> e2%*%t(e1)/sum(e2*e1)
[,1] [,2] [,3] [,4] [,5]
[1,] 0.3723509+0i 0.16493105+0i 0.12228844+0i 0.07654045+0i 0.04938080+0i
[2,] 0.5815983+0i 0.25761620+0i 0.19101002+0i 0.11955335+0i 0.07713098+0i
[3,] 0.5087682+0i 0.22535649+0i 0.16709099+0i 0.10458241+0i 0.06747233+0i
[4,] 0.4863344+0i 0.21541951+0i 0.15972320+0i 0.09997091+0i 0.06449717+0i
[5,] 0.4370443+0i 0.19358672+0i 0.14353524+0i 0.08983884+0i 0.05796038+0i
[6,] 0.3775498+0i 0.16723388+0i 0.12399588+0i 0.07760914+0i 0.05007027+0i
[7,] 0.2043711+0i 0.09052521+0i 0.06712009+0i 0.04201053+0i 0.02710349+0i
[,6] [,7]
[1,] 0.03043199+0i 0.02578726+0i
[2,] 0.04753364+0i 0.04027875+0i
[3,] 0.04158129+0i 0.03523489+0i
[4,] 0.03974778+0i 0.03368122+0i
[5,] 0.03571934+0i 0.03026763+0i
[6,] 0.03085689+0i 0.02614731+0i
[7,] 0.01670311+0i 0.01415378+0i
てことで、元のニジマスの感度行列とelasticity行列を計算してみます。
> v%*%t(w)/sum(v*w)
[,1] [,2] [,3] [,4]
[1,] 0.3425195+0i 0.01240939+0i 0.001393725+0i 0.0001464334+0i
[2,] 9.4541008+0i 0.34251950+0i 0.038469104+0i 0.0040418030+0i
[3,] 49.9250531+0i 1.80877110+0i 0.203146983+0i 0.0213438839+0i
[4,] 240.1378128+0i 8.70012766+0i 0.977130103+0i 0.1026633580+0i
[5,] 373.7509135+0i 13.54089396+0i 1.520807009+0i 0.1597854307+0i
[6,] 617.9583878+0i 22.38846435+0i 2.514496723+0i 0.2641886443+0i
[7,] 673.0852259+0i 24.38569470+0i 2.738809972+0i 0.2877563875+0i
[,5] [,6] [,7]
[1,] 7.639550e-06+0i 4.262394e-07+0i 2.316381e-08+0i
[2,] 2.108641e-04+0i 1.176491e-05+0i 6.393591e-07+0i
[3,] 1.113528e-03+0i 6.212792e-05+0i 3.376316e-06+0i
[4,] 5.356030e-03+0i 2.988332e-04+0i 1.623997e-05+0i
[5,] 8.336135e-03+0i 4.651045e-04+0i 2.527591e-05+0i
[6,] 1.378294e-02+0i 7.690021e-04+0i 4.179110e-05+0i
[7,] 1.501248e-02+0i 8.376032e-04+0i 4.551920e-05+0i
(追記その2:2015.02.17)
不安なので、Caswell, 1978のデータを使ってRでの計算方法が合っているのか検証。ナベナDipsacus sylvestrisの射影行列。
> T <- matrix(c(0,0.75,0,0.01,0.07,0.002,0, 0,0,0.97,0.01,0.01,0.01,0, 0,0,0,0.01,0,0,0, 0,0,0,0.13,0.13,0.04,0, 0,0,0,0,0.24,0.25,0.02, 0,0,0,0,0,0.17,0.75, 431,0,0,0,0,0,0), nrow=7,ncol=7)
> T
[,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] 0.000 0.00 0.00 0.00 0.00 0.00 431
[2,] 0.750 0.00 0.00 0.00 0.00 0.00 0
[3,] 0.000 0.97 0.00 0.00 0.00 0.00 0
[4,] 0.010 0.01 0.01 0.13 0.00 0.00 0
[5,] 0.070 0.01 0.00 0.13 0.24 0.00 0
[6,] 0.002 0.01 0.00 0.04 0.25 0.17 0
[7,] 0.000 0.00 0.00 0.00 0.02 0.75 0
> ww<-eigen(T)$vectors[,1]
> ww
[1] -0.914269286+0i -0.359121206+0i -0.182439319+0i -0.008181629+0i
[5] -0.041125039+0i -0.009214890+0i -0.004050337+0i> vv<-eigen(t(T))$vectors[,1]
> vv
[1] -4.057618e-03+0i -2.546141e-03+0i -7.332412e-05+0i -1.400042e-02+0i
[5] -7.011575e-02+0i -3.949287e-01+0i -9.159127e-01+0i> Re(vv)%*%t(Re(ww))/sum(Re(vv)*Re(ww))
[,1] [,2] [,3] [,4] [,5]
[1,] 0.247572111 0.097245305 4.940217e-02 0.0022154777 0.0111361202
[2,] 0.155350642 0.061021092 3.099969e-02 0.0013902046 0.0069878768
[3,] 0.004473809 0.001757294 8.927333e-04 0.0000400353 0.0002012378
[4,] 0.854223953 0.335535647 1.704575e-01 0.0076442943 0.0384241204
[5,] 4.278052628 1.680401437 8.536708e-01 0.0382835127 0.1924324515
[6,] 24.096239608 9.464903587 4.808322e+00 0.2156328532 1.0838806491
[7,] 55.883635005 21.950861462 1.115139e+01 0.5000924568 2.5137196330
[,6] [,7]
[1,] 2.495271e-03 1.096778e-03
[2,] 1.565774e-03 6.882245e-04
[3,] 4.509137e-05 1.981958e-05
[4,] 8.609695e-03 3.784328e-03
[5,] 4.311835e-02 1.895236e-02
[6,] 2.428652e-01 1.067496e-01
[7,] 5.632493e-01 2.475721e-01
なぜでしょう・・・。Caswell, 1978が求めている感度行列と、オーダーは一緒なのに値が微妙に違います。浮動小数点の計算誤差か。
(追記その3:2015.02.20)
計算誤差の話はとりあえず棚上げして、今度はファットヘッドミノーの生命表(Miler and Ankley, 2004)から、感度行列を作成してみました。
> A <- matrix(c(0.75,0.39,0, 1.5,0,0.39, 3,0,0), nrow=3, ncol=3)
> A
[,1] [,2] [,3]
[1,] 0.75 1.50 3
[2,] 0.39 0.00 0
[3,] 0.00 0.39 0> w <- eigen(A)$vectors [,1]
> v <- eigen(t(A))$vectors [,1]
> lamda<-Re(eigen(A)$values [1])
> lamda
[1] 1.400407> Sensitivity <- round(v %*%t(w)/sum(v*w), 2)
> Sensitivity
[,1] [,2] [,3]
[1,] 0.61 0.17 0.05
[2,] 1.02 0.28 0.08
[3,] 1.31 0.37 0.10> Elasticity<-round(Sensitivity*A/lamda,2)
> Elasticity
[,1] [,2] [,3]
[1,] 0.33 0.18 0.11
[2,] 0.28 0.00 0.00
[3,] 0.00 0.10 0.00
3齢目のミノーは多産ですが、その産仔数が個体群増加に与える影響は他のパラメータに比べると大きくないことが分かります。